Abstract
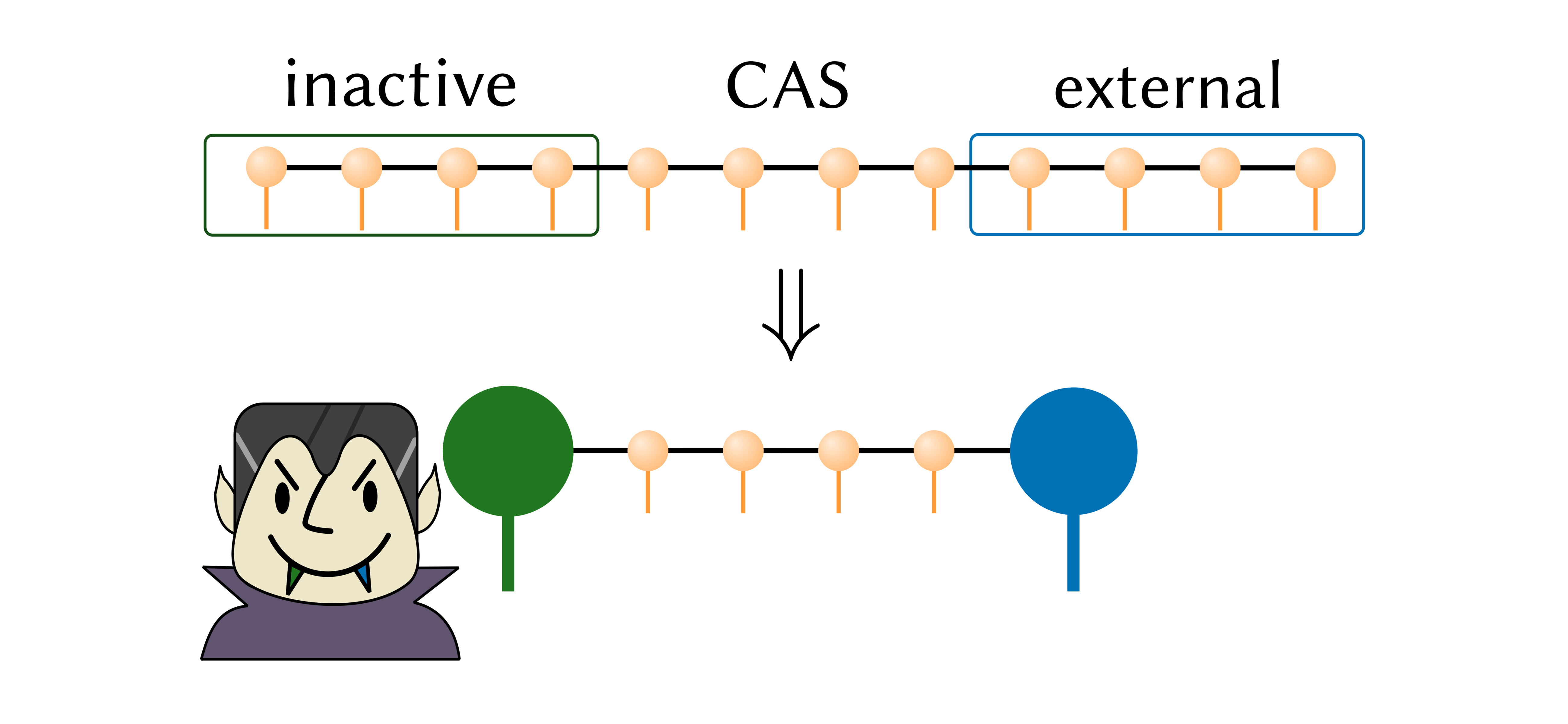
We explore various ways to group orbitals into clusters in a matrix product state (MPS). We explain how a generic cluster MPS can often lead to an increase in computational cost and instead propose a special cluster structure, involving only the first and last orbitals/sites, with a wider scope for computational advantage. This structure is a natural formalism to describe correlated multireference (MR) theories. We demonstrate the flexibility and usefulness of this approach by implementing various uncontracted MR configuration interaction, perturbation and linearized coupled cluster theories using an MPS with large cluster sites. Applications to the nitrogen dimer, the chromium dimer, and benzene, including up to triple excitations in the external space, demonstrate the utility of an MPS with up to two large sites. We use our results to analyze the quality of different multireference approximations.