Abstract
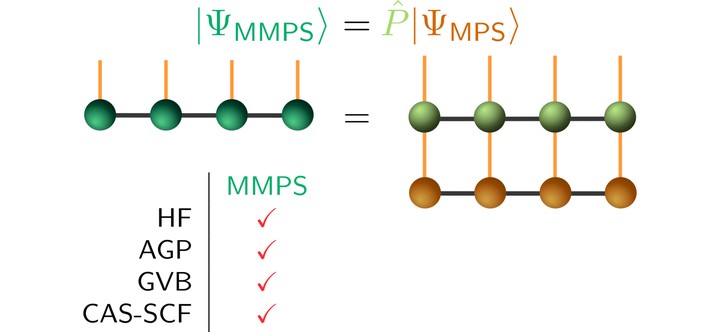
During my postdoctoral studies in the group of Prof. G. Chan (Caltech), I explored new ways to apply the density matrix renormalization group (DMRG) to bigger systems. In this article we explore a class of simple, qualitative wavefunctions, the minimal matrix product state (MMPS), which combines projection operators and the DMRG in order to yield a low-scaling method for quick explorations of the potential energy landscape of strongly correlated systems. Without jeopardizing low computational cost, MMPSs generalize well-established methods such as the projected Hartree-Fock-Bogoliubov (HFB)/antisymmetrized geminal power (AGP) method and the generalized valence bond (GVB) method. For the systems we studied, we show that MMPSs give correct qualitative behavior across the whole PES, often significantly improving aforementioned ansätze.