Abstract
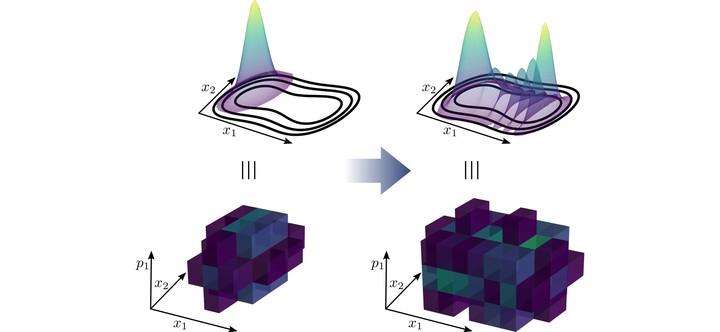
The main project of my PhD studies (in the groups of Prof. B. Hartke and Prof. D. Tannor) was the exploitation of sparsity in vibrational and electronic wavefunctions. Exploiting the sparsity means pruning of the underlying basis. This is similar to selected CI techniques for electronic structure calculations. However, here, pruning was used for solving the time-dependent Schrödinger equation. Since the wavefunction changes with time, also the sparsity pattern changes such that the pruning has to be done dynamically. In this publication, for the first time, I could show that pruning actually is faster than conventional methods. This was only possible by developing new algorithms adapted to the pruned basis and by identifying certain requirements the employed basis has to fulfill, most importantly orthogonality, in order to achieve an efficient algorithm. The developed algorithms deal with the update of the sparsity pattern and with the computation of the action of an operator onto a wavefunction. This can be understood as a transformation of sparse, high-dimensional tensors. Parts of the algorithms I developed are now used in the group of Prof. T. Carrington (Queen’s University) [1], who is one of the lead-developers of methods based on pruning.