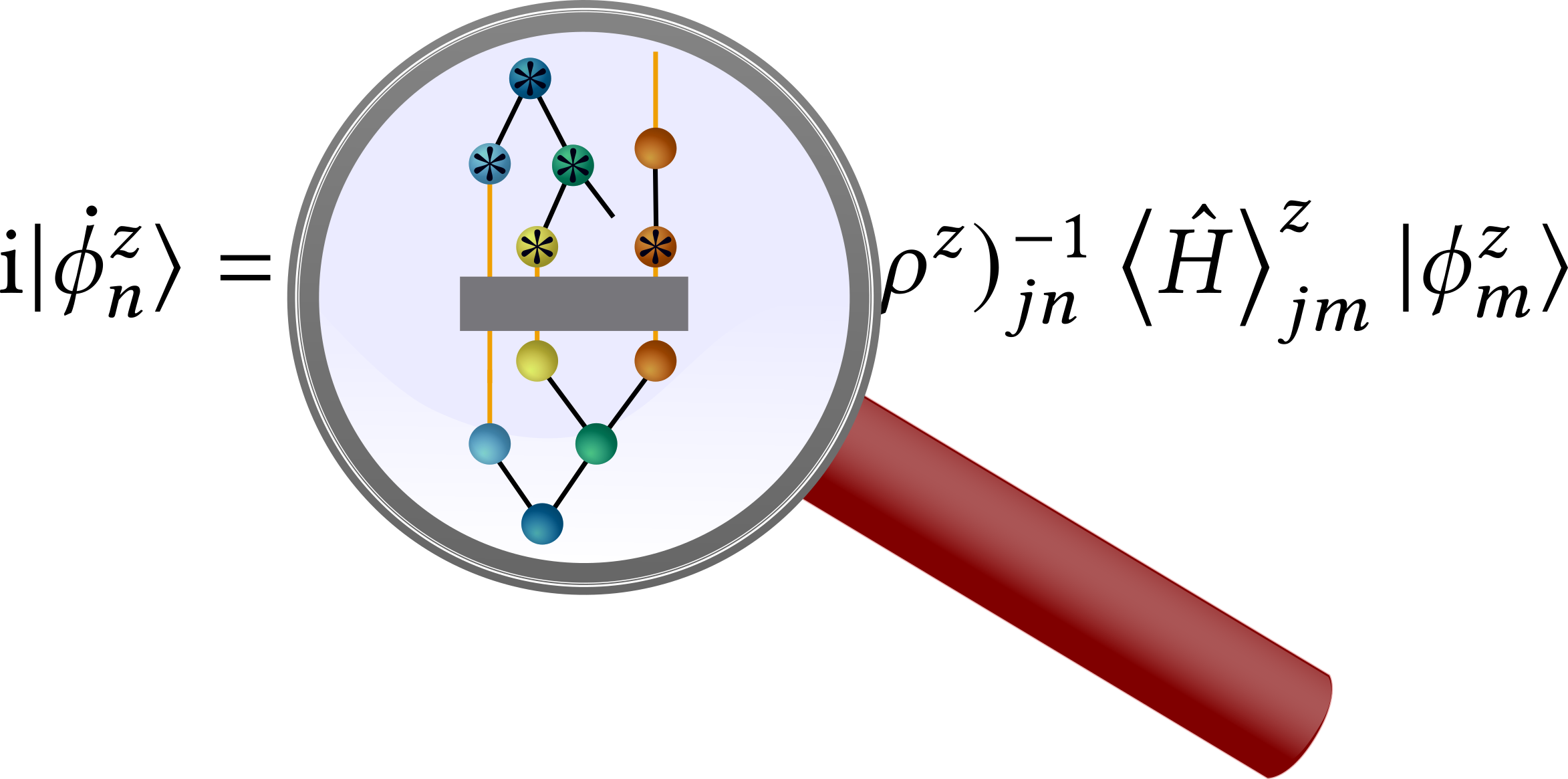
Abstract
The multilayer multiconfiguration time-dependent Hartree (ML-MCTDH) method and the density matrix renormalization group (DMRG) are powerful workhorses applied mostly in different scientific fields. Although both methods are based on tensor network states, very different mathematical languages are used for describing them. This severely limits knowledge transfer and sometimes leads to re-inventions of ideas well known in the other field. Here, we review ML-MCTDH and DMRG theory using both MCTDH expressions and tensor network diagrams. We derive the ML-MCTDH equations of motions using diagrams and compare them with time-dependent and time-independent DMRG algorithms. We further review two selected recent advancements. The first advancement is related to optimizing unoccupied single-particle functions in MCTDH, which corresponds to subspace enrichment in the DMRG. The second one is related to finding optimal tree structures and on highlighting similarities and differences of MCTDH and DMRG theories. We hope that this contribution will foster more fruitful cross-fertilization of ideas between ML-MCTDH and DMRG.