We explore the lowest mass limit that can be placed on the halo mass function in CDM using 28 strong gravitational lenses. For this purpose, we study an extreme model in which the halo mass function and mass-concentration relation follow CDM, with a sharp cutoff at some mass scale, m_low. Lensing provides a unique window into this quantity as it does not depend on the presence of baryons in dark matter halos and also allows the detection of low-mass halos at cosmological distances, both in the lens galaxies and along the line of sight. Our model incorporates the effects of tidal stripping of subhalos, leading to the presence of many subhalos below a given model cutoff scale. We place an upper limit on the low-mass cutoff of the halo mass function of m_low < 10^8.3 M⊙ at 10:1 odds using a prior for the normalization of the subhalo mass function from the semi-analytic model galacticus and m_low < 10^8.2 M⊙ at 10:1 odds using a prior from N-body simulations. These limits are comparable to, or stronger than, existing constraints based on Milky Way satellite galaxies. Based on these results, we forecast more than an order of magnitude improvement with a sample of 200 quadruply imaged quasar lenses. This number represents a small subset of the thousands that are anticipated to be discovered by Rubin, Euclid, and Roman. Furthermore, with this larger sample of lenses we expect to directly constrain the normalization of the subhalo mass function, thereby eliminating a major source of uncertainty in our current measurements.

Over the past decade, the Python-based Simulations of Chemistry Framework (PySCF) has developed into a widely used open-source platform for electronic structure theory and quantum chemical method development. This article reviews the major advances since the previous overview in 2020, covering new modules and methodology, infrastructure changes, and performance benchmarks.

For decades, scientists have studied the intricate charge migration dynamics, where after ionization a localized charge distribution (‘hole’) migrates across the molecule on a femtosecond timescale. This has the potential for controlling electrons in molecules, yet a comprehensive understanding of the many aspects of charge migration is still missing. In this work, we analyze charge migration using an extension of localized intrinsic bond orbitals (IBOs). These orbitals lead to a compact representation of the dynamics and map the complex, correlated many-electron charge migration to chemical concepts such as curly arrows and orbital-orbital interactions. By analyzing multiple challenging scenarios, we show how IBOs enable us to identify key mechanisms in charge migration. For example, we show that different mechanisms are responsible for converting a π-shaped hole to a σ-shaped hole and vice versa. We explain these in terms of hyperconjugation interactions and configurations that couple orbitals with different symmetries. We further demonstrate how IBOs can be used to find molecules with high charge migration efficiency. We carry out all simulations using an efficient set up of the time-dependent density matrix renormalization group (TDDMRG), correlating as many as 45 electrons in 50 orbitals. We believe that our results will be useful to design future experiments. The proposed IBO analysis is applicable to other types of real-time electron dynamics and spectroscopy.

We present the full sample of measurements of the warm dust emission of 31 strongly lensed, multiply imaged quasars, observed with JWST MIRI multiband imaging, which we use to constrain the particle properties of dark matter. The strongly lensed warm dust region of quasars is compact and statistically sensitive to a population of dark matter halos down to masses of 10^6 M⊙. The high spatial resolution and infrared sensitivity of MIRI make it uniquely suited to measure multiply imaged warm dust emission from quasars and thus to infer the properties of low-mass dark halos. We use the measured flux ratios to test for a warm dark matter turnover in the halo mass function. To infer the dark matter parameters, we use a forward modeling pipeline which explores dark matter parameters while also accounting for tidal stripping effects on subhalos, globular clusters, and complex deflector macromodels with m = 1, m = 3, and m = 4 elliptical multipole moments. Adopting a comparable prior on the projected density of substructure to our previous analyses, the data presented here provide a factor of 2 improvement in sensitivity to a turnover in the halo mass function. Assuming subhalo abundance predicted by the semi-analytic model galacticus we infer, with a Bayes factor of 10:1, a half-mode mass m_hm < 10^7.8 M⊙ (m > 5.6 keV for a thermally produced dark matter particle). If instead we use a prior from N-body simulations, we infer m_hm < 10^7.6 M⊙ (m > 6.4 keV). This is one of the strongest constraints to date on a turnover on the halo mass function, and the flux ratios and inference methodology presented here can be used to test a broad range of dark matter physics.

To understand the dynamics of quantum many-body systems, it is essential to study excited eigenstates. While tensor network states have become a standard tool for computing ground states in computational many-body physics, obtaining accurate excited eigenstates remains a significant challenge. In this work, we develop an approach that combines the inexact Lanczos method, which is designed for efficient computation of excited states, with tree tensor network states (TTNSs). We demonstrate our approach by computing excited vibrational states for three challenging problems: (1) 122 states in two different energy intervals of acetonitrile (12-dimensional), (2) Fermi resonance states of the fluxional Zundel ion (15-dimensional),and (3) selected excited states of the fluxional and very correlated Eigen ion (33-dimensional). The proposed TTNS inexact Lanczos method is directly applicable to other quantum many-body systems.

Accurate vibrational spectra are essential for understanding how molecules behave, yet their computation remains challenging and benchmark data to reliably compare different methods are sparse. Here, we present high-accuracy eigenstate computations for the six-atom, 12-dimensional acetonitrile molecule, a prototypical, strongly coupled, anharmonic system. Using a density matrix renormalization group (DMRG) algorithm with a tree-tensor-network-state (TTNS) ansatz, a refinement using TTNSs as basis set, and reliable procedures to estimate energy errors, we compute up to 5,000 vibrational states with error estimates below 0.0007 cm-1. Our analysis reveals that previous works underestimated the energy error by up to two orders of magnitude. Our data serve as a benchmark for future vibrational spectroscopy methods and our new method offers a path toward similarly precise computations of large, complex molecular systems.

Compared to ground state electronic structure optimizations, accurate simulations of molecular real-time electron dynamics are usually much more difficult to perform. To simulate electron dynamics, the time-dependent density matrix renormalization group (TDDMRG) has been shown to offer an attractive compromise between accuracy and cost. However, many simulation parameters significantly affect the quality and efficiency of a TDDMRG simulation. So far, it is unclear whether common wisdom from ground state DMRG carries over to the TDDMRG, and a guideline on how to choose these parameters is missing. Here, in order to establish such a guideline, we investigate the convergence behavior of the main TDDMRG simulation parameters, such as time integrator, the choice of orbitals, and the choice of matrix-product-state representation for complex-valued non-singlet states. In addition, we propose a method to select orbitals that are tailored to optimize the dynamics. Lastly, we showcase the TDDMRG by applying it to charge migration ionization dynamics in furfural, where we reveal a rapid conversion from an ionized state with a σ character to one with a π character within less than a femtosecond.

The nitrate radical NO3 plays an important role in atmospheric chemistry, yet many aspects of its coupled and anharmonic vibronic structure remain elusive. Here, using an accurate, coupled full-dimensional diabatic potential that includes five electronic states, we revisit the vibronic spectrum associated with the electronic X~2A′2 state. Using recently developed tensor network state methods, we are able to compute more than 2500 vibronic states, thereby increasing the number of computed full-dimensional states by a factor of 50, compared to previous work. While we obtain good agreement with experiment for most of the assigned vibronic levels, for several others, we observe striking disagreement. Further, for the antisymmetric bending motion we find remarkably large symmetry-induced level splittings that are larger than the zero-order reference. We discuss non-negligible nonadiabatic effects and show that the Born-Oppenheimer approximation leads to significant errors in the spectrum.

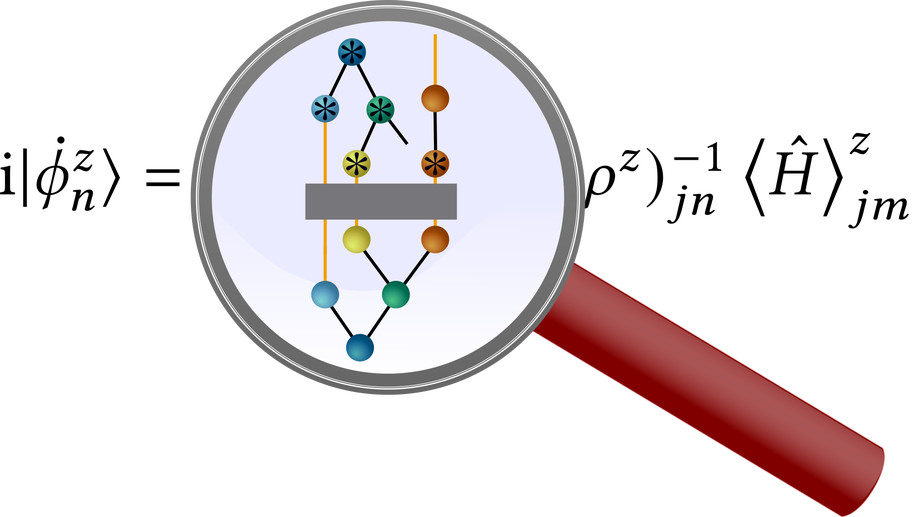
The multilayer multiconfiguration time-dependent Hartree (ML-MCTDH) method and the density matrix renormalization group (DMRG) are powerful workhorses applied mostly in different scientific fields. Although both methods are based on tensor network states, very different mathematical languages are used for describing them. This severely limits knowledge transfer and sometimes leads to re-inventions of ideas well known in the other field. Here, we review ML-MCTDH and DMRG theory using both MCTDH expressions and tensor network diagrams. We derive the ML-MCTDH equations of motions using diagrams and compare them with time-dependent and time-independent DMRG algorithms. We further review two selected recent advancements. The first advancement is related to optimizing unoccupied single-particle functions in MCTDH, which corresponds to subspace enrichment in the DMRG. The second one is related to finding optimal tree structures and on highlighting similarities and differences of MCTDH and DMRG theories. We hope that this contribution will foster more fruitful cross-fertilization of ideas between ML-MCTDH and DMRG.

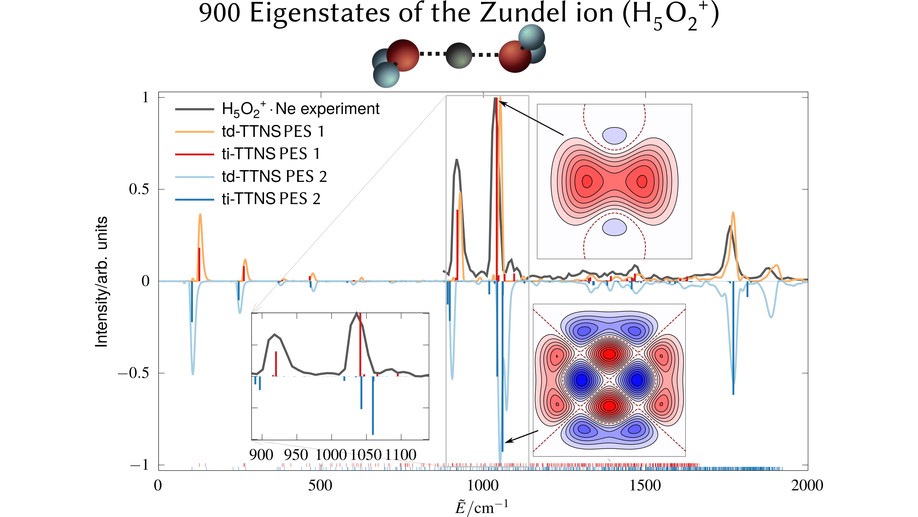
The infrared (IR) spectra of protonated water clusters encode precise information on the dynamics and structure of the hydrated proton. However, the strong anharmonic coupling and quantum effects of these elusive species remain puzzling up to the present day. Here, we report unequivocal evidence that the interplay between the proton transfer and the water wagging motions in the protonated water dimer (Zundel ion) giving rise to the characteristic doublet peak is both more complex and more sensitive to subtle energetic changes than previously thought. In particular, hitherto overlooked low- intensity satellite peaks in the experimental spectrum are now unveiled and mechanistically assigned. Our findings rely on the comparison of IR spectra obtained using two highly accurate potential energy surfaces (PESs) in conjunction with highly accurate state-resolved quantum simulations. We demonstrate that these high-accuracy simulations are important for providing definite assignments of the complex IR signals of fluxional molecules.

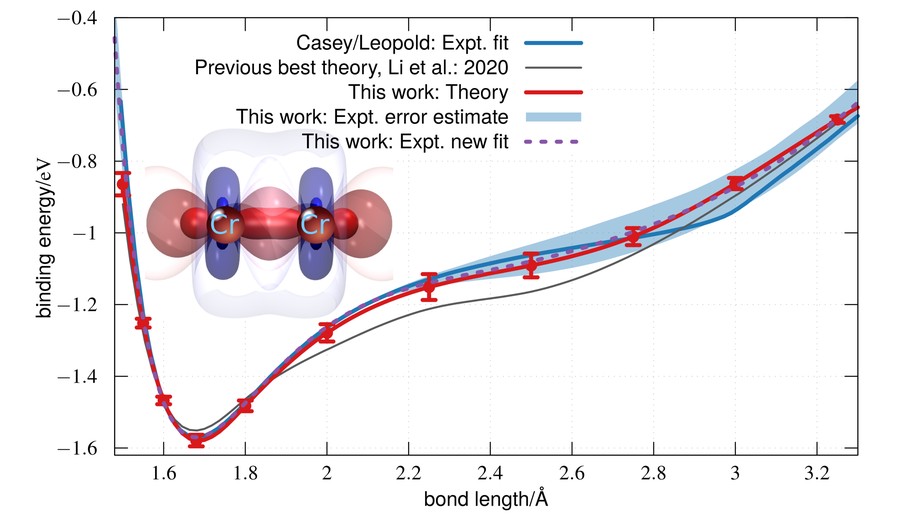
The complex electronic structure and unusual potential energy curve of the chromium dimer have fascinated scientists for decades, with agreement between theory and experiment so far elusive. Here, we present a new ab initio simulation of the potential energy curve and vibrational spectrum that significantly improves on all earlier estimates. Our data support a shift in earlier experimental assignments of a cluster of vibrational frequencies by one quantum number. The new vibrational assignment yields an experimentally derived potential energy curve in quantitative agreement with theory across all bond lengths and across all measured frequencies. By solving this long-standing problem, our results raise the possibility of quantitative quantum chemical modeling of transition metal clusters with spectroscopic accuracy.

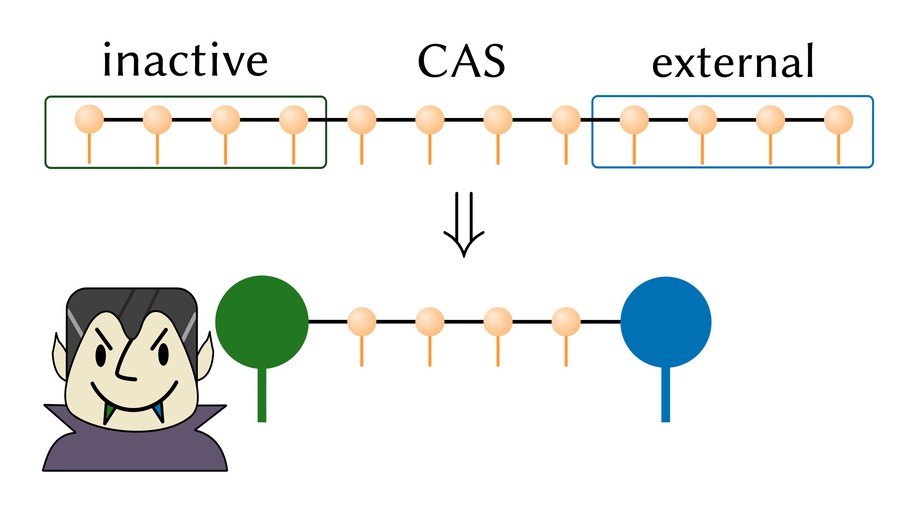
We explore various ways to group orbitals into clusters in a matrix product state (MPS). We explain how a generic cluster MPS can often lead to an increase in computational cost and instead propose a special cluster structure, involving only the first and last orbitals/sites, with a wider scope for computational advantage. This structure is a natural formalism to describe correlated multireference (MR) theories. We demonstrate the flexibility and usefulness of this approach by implementing various uncontracted MR configuration interaction, perturbation and linearized coupled cluster theories using an MPS with large cluster sites. Applications to the nitrogen dimer, the chromium dimer, and benzene, including up to triple excitations in the external space, demonstrate the utility of an MPS with up to two large sites. We use our results to analyze the quality of different multireference approximations.

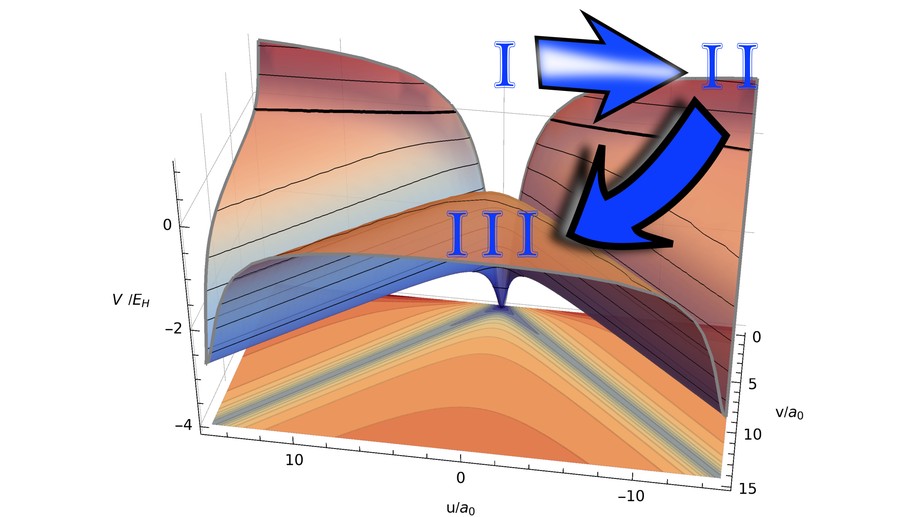
Our article sheds light on the control of the motion of the ionized electrons during double ionization. To first order, the field only drives the electron into the same direction (front-to-back motion). In this paper, our goal was to achieve the opposite, back-to-back motion, where both electrons are ejected into opposite directions. This is only possible via an interplay between the inter-particle forces and the potential. By extensive usage of four different control procedures (local control, derivative-free optimizations of basis expansions, Krotov method, and control of the classical equations of motions), we could identify pulse characteristics that lead to the desired back-to-back motion. Additionally, we were able to identify a simple, classical two-step mechanism. Besides these new physical results, this contribution also discusses new methodologies for using local control procedures for this difficult system and employs a new method to efficiently propagate the wavefunction in time [H. R. Larsson, B. Hartke and D. J. Tannor, J. Chem. Phys., 145, 204108 (2016)].

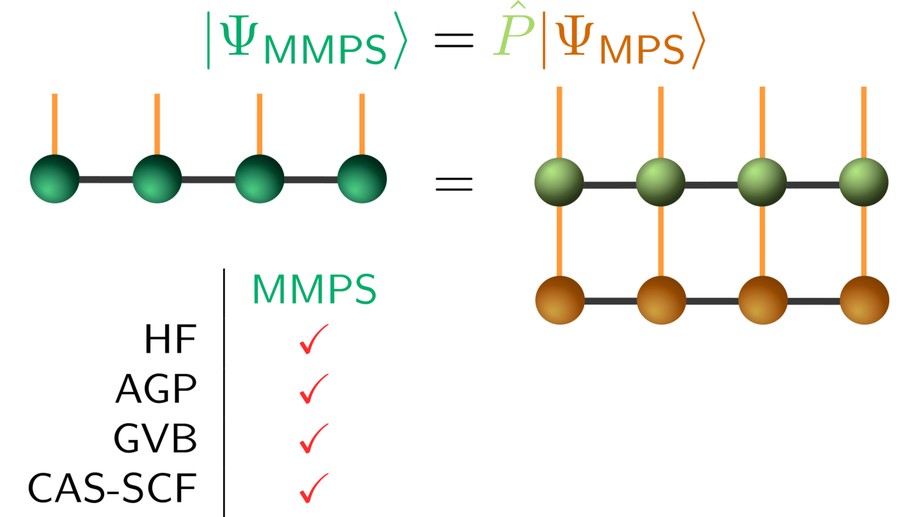
During my postdoctoral studies in the group of Prof. G. Chan (Caltech), I explored new ways to apply the density matrix renormalization group (DMRG) to bigger systems. In this article we explore a class of simple, qualitative wavefunctions, the minimal matrix product state (MMPS), which combines projection operators and the DMRG in order to yield a low-scaling method for quick explorations of the potential energy landscape of strongly correlated systems. Without jeopardizing low computational cost, MMPSs generalize well-established methods such as the projected Hartree-Fock-Bogoliubov (HFB)/antisymmetrized geminal power (AGP) method and the generalized valence bond (GVB) method. For the systems we studied, we show that MMPSs give correct qualitative behavior across the whole PES, often significantly improving aforementioned ansätze.

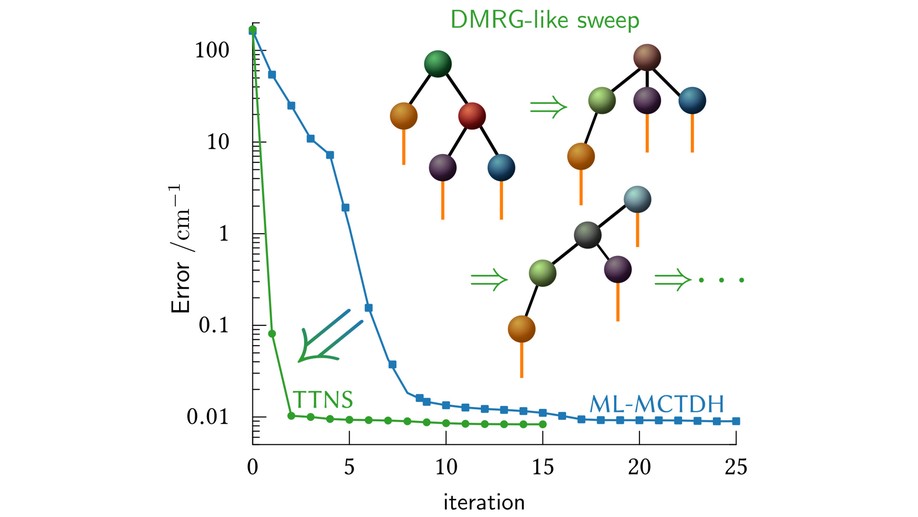
During my postdoctoral studies in the group of Prof. G. Chan (Caltech), as side project, I worked on the computation of vibrational spectra using tree-tensor network states (TTNS). There, I applied methods developed in the condensed matter community to molecular systems. Compared to established approaches for computing vibrational spectra, such as the multilayer multiconfiguration time-dependent Hartree (ML-MCTDH) method, the new approach is faster and much more robust and the diagrammatic language from condensed matter physics I use gains much more insights. I am currently working on using the TTNS method to compute high-lying vibrational states of the Zundel ion.

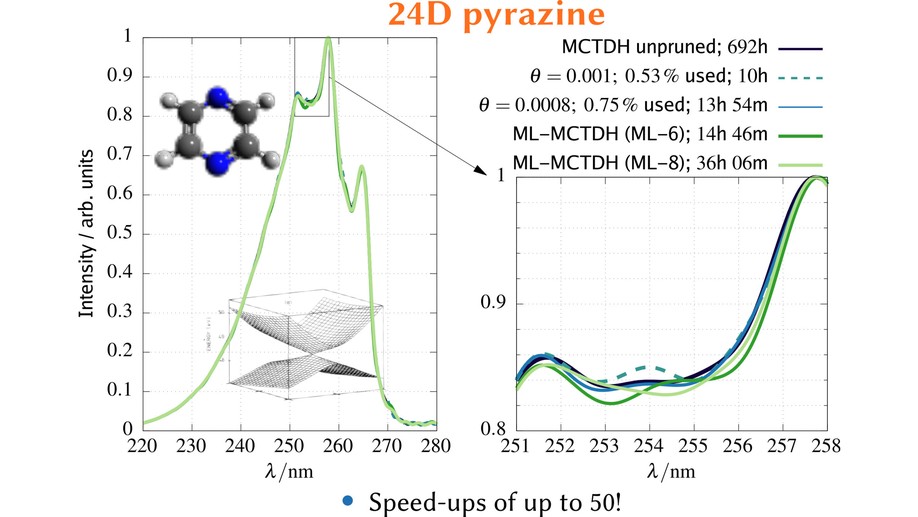
The main project of my PhD studies (in the groups of Prof. B. Hartke and Prof. D. Tannor) was the exploitation of sparsity in vibrational and electronic wavefunctions. Exploiting the sparsity means pruning of the underlying basis. This is similar to selected CI techniques for electronic structure calculations. Particularly successful was the application of dynamical pruning to the multiconfiguration time-dependent Hartree (MCTDH) method. While simple static pruning has already been studied 20 years ago by Worth [1], the conclusions from this mainly was that even static pruning requires too much bookkeeping such that this approach has quickly been abandoned. Due to this experience, many MCTDH developers advised me against developing methods based on pruning. Instead, I started working on a completely new MCTDH implementation with pruning. This was successful and the developed methods were applied to up to 24-dimensional systems and were up to 50 times faster than conventional MCTDH and competitive with state-of-the-art but more complicated multilayer MCTDH. The reasons for this speedup are newly developed algorithms, an efficient implementation, and a dynamical pruning instead of a simple static one. Furthermore, I applied, also for the first time, dynamical pruning both to the orbitals and the underlying grid representation. This means that the used basis changes at each time step at two different levels.

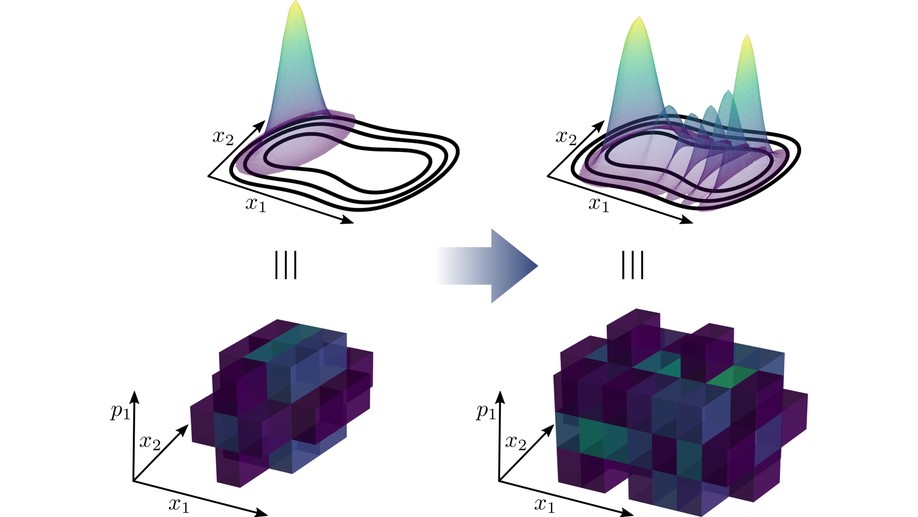
The main project of my PhD studies (in the groups of Prof. B. Hartke and Prof. D. Tannor) was the exploitation of sparsity in vibrational and electronic wavefunctions. Exploiting the sparsity means pruning of the underlying basis. This is similar to selected CI techniques for electronic structure calculations. However, here, pruning was used for solving the time-dependent Schrödinger equation. Since the wavefunction changes with time, also the sparsity pattern changes such that the pruning has to be done dynamically. In this publication, for the first time, I could show that pruning actually is faster than conventional methods. This was only possible by developing new algorithms adapted to the pruned basis and by identifying certain requirements the employed basis has to fulfill, most importantly orthogonality, in order to achieve an efficient algorithm. The developed algorithms deal with the update of the sparsity pattern and with the computation of the action of an operator onto a wavefunction. This can be understood as a transformation of sparse, high-dimensional tensors. Parts of the algorithms I developed are now used in the group of Prof. T. Carrington (Queen’s University) [1], who is one of the lead-developers of methods based on pruning.

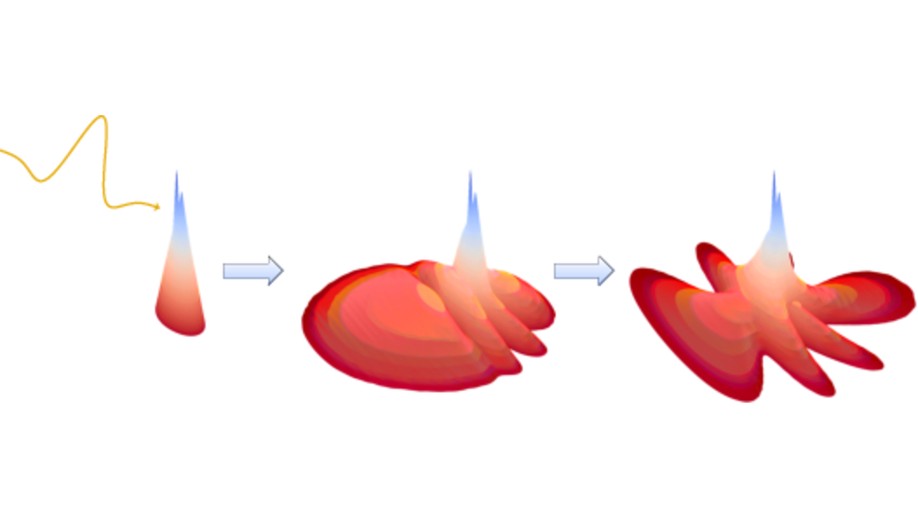
During my Master’s studies (in the group of Prof. M. Bonitz, Kiel University), I performed electron dynamics simulations utilizing a time-dependent multireference configuration interaction (TD-MR-CI) method. This method reduces the computational effort by considering only a selection of relevant configurations needed to describe the wavefunction, based on physical insights into the problem. With the help of a well-chosen coordinate system and a careful optimization of tensor transformations appearing in this method (more than 50,000 basis functions can be used), I could improve the methodology such that I was able to unravel correlation effects that occur during ionization dynamics of LiH in strong and short laser fields. In particular, I could show that, for intermediate field intensities, qualitatively wrong results are predicted if methods that are too simple are employed that take no correlation into account. My code is now used in the group of Prof. L. Madsen (Aarhus University) [1] [2].

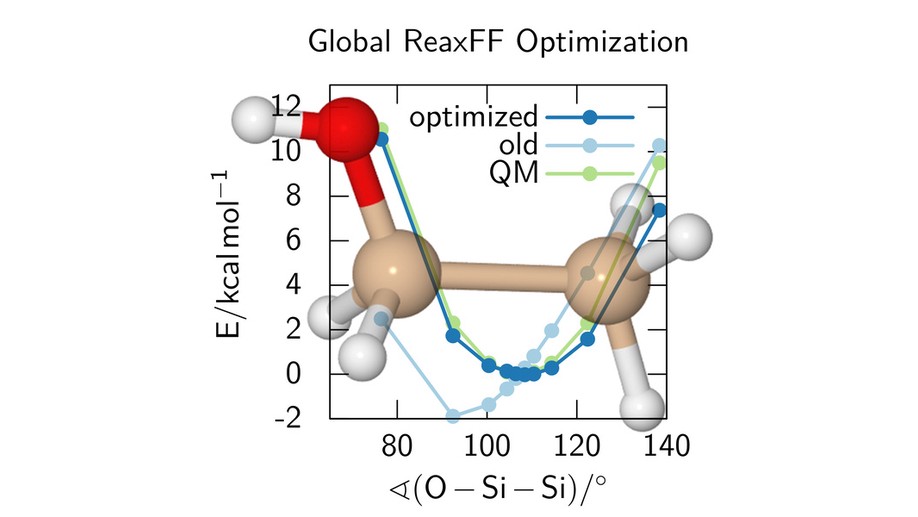
In my Bachelor’s studies (in the group of Prof. B. Hartke, Kiel University), I performed global optimization of the reactive force field ReaxFF. The development of force fields that are able to describe any chemical reactions is a highly complex task and the optimization of the parameters of the force fields is very demanding, due to the sheer number of parameters (up to 300), their strong and partially non-obvious interdependencies, and the complicated, highly nonlinear and rugged function that needs to be globally optimized. Analytic derivatives with respect to the parameters are typically not available. Despite these challenges, I successfully performed global optimization of ReaxFF for systems containing containing Si, O and H. My optimized force field outperformed that of the lead developer of ReaxFF.